Have you ever watched a pendulum swing back and forth, mesmerized by its rhythmic motion? Perhaps you wondered, “What makes one pendulum swing faster than another?” It’s a question that delves into the fascinating world of physics, where the interplay of forces determines the speed and behavior of objects in motion. In this exploration, we’ll delve into the factors that influence a pendulum’s maximum speed, understanding how its length, mass, and initial displacement affect its dynamic journey.
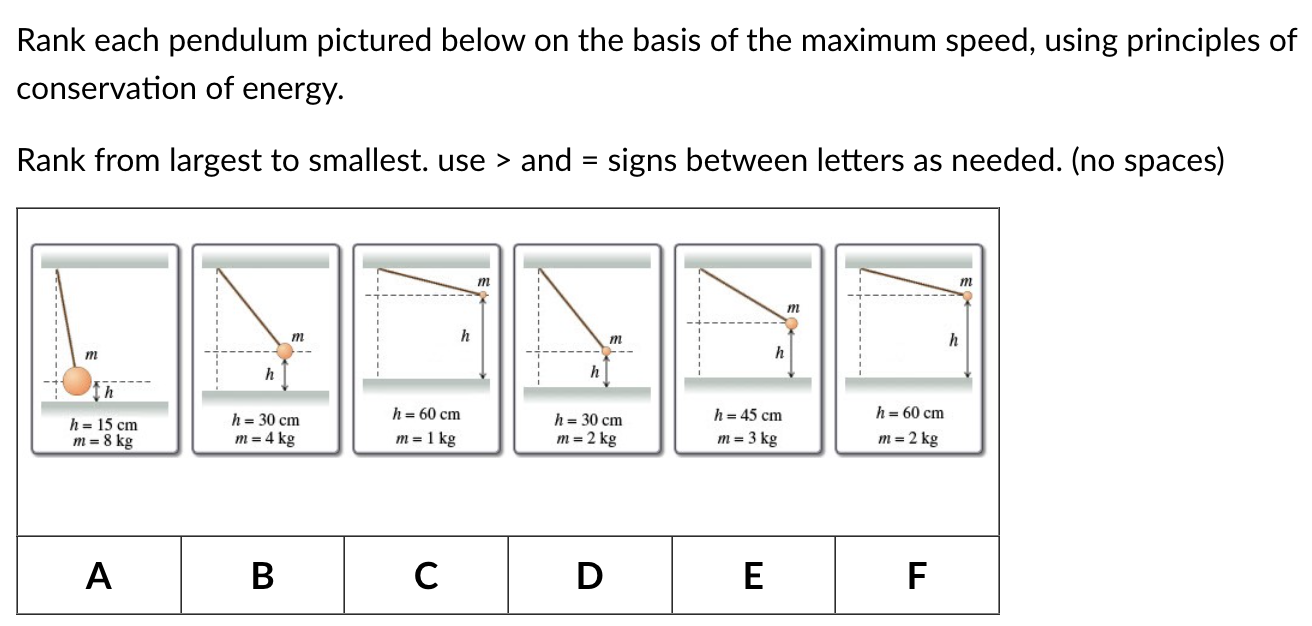
Image: www.solutionspile.com
Imagine standing in a science museum, captivated by a towering pendulum that seems to take forever to complete its swing. Now, picture a tiny pendulum in a grandfather clock, ticking away with unwavering precision. The striking contrast in their movements highlights the fundamental principle that governs pendulums: the longer the pendulum, the slower its swing. Yet, there’s more to the story than just length. The interplay of mass, initial displacement, and, of course, gravity itself are all crucial factors in determining a pendulum’s maximum speed. Let’s unravel the mysteries behind these factors and unlock the secrets of a pendulum’s captivating motion.
The Physics of Pendulum Motion
At the heart of a pendulum’s motion lies the concept of **simple harmonic motion**. This type of motion is characterized by a repeating back-and-forth movement around an equilibrium point, often described as a sinusoidal wave. For a pendulum, the equilibrium point is its resting position, where it hangs vertically. As the pendulum swings, it experiences a restoring force that continuously pulls it back towards this equilibrium position, driving its oscillatory behavior.
The restoring force acting on a pendulum is due to gravity. When the pendulum is displaced from its equilibrium position, gravity acts upon it, trying to return it to its hanging position. This gravitational force is what drives the pendulum’s swing. The larger the displacement, the greater the force, leading to a faster swing.
Factors Influencing Pendulum Speed
The speed of a pendulum is determined by a combination of factors:
- Length (L): The primary factor influencing a pendulum’s period (time for one complete swing) is its length. Longer pendulums have longer periods, meaning they swing more slowly. This relationship is inverse—as length increases, period increases, and speed decreases.
- Mass (m): The mass of the bob (the weight at the end of the pendulum) has no impact on the period or the speed. The reason for this is that the gravitational force acting on the bob is directly proportional to its mass. Therefore, a heavier bob experiences a stronger force but also has a greater inertia, resulting in a balanced effect on the period and speed.
- Initial Displacement (θ): The initial displacement, or angle, from which the pendulum is released significantly influences its maximum speed. A larger initial displacement results in the bob having a greater *potential energy* at the start. This energy is converted into *kinetic energy* as the bob swings downwards, reaching its highest speed at the bottom of its arc. A larger initial displacement equates to a larger initial potential energy, subsequently leading to a higher maximum speed.
- Gravity (g): The acceleration due to gravity on Earth influences the pendulum’s period and speed. The stronger the gravitational force, the faster the pendulum swings. If we were to take a pendulum to the moon, where gravity is weaker than on Earth, it would swing more slowly.
Understanding Maximum Speed
A pendulum’s maximum speed occurs at the *lowest point* of its swing. This is because its potential energy (due to height) is fully converted into kinetic energy (due to motion) at this point. The steeper the initial displacement, the greater the initial potential energy, leading to a higher maximum speed.
To illustrate this, consider a pendulum swinging with a small initial displacement. It doesn’t gain much speed before swinging back up. However, if we release it from a significantly larger angle, it will have a much larger maximum speed at the bottom of its swing. This is similar to a skateboarder going down a ramp; the higher the ramp, the faster the skater will travel at the bottom.

Image: zuoti.pro
Ranking Pendulums by Maximum Speed
Now that we understand the factors influencing pendulum speed, let’s rank several pendulums based on their maximum speed:
Scenario: Four Pendulums
Imagine we have four pendulums, each with different characteristics (assuming all are released from the same initial displacement angle):
| Pendulum | Length (L) | Mass (m) | Maximum Speed |
|---|---|---|---|
| Pendulum A | 1 meter | 1 kg | |
| Pendulum B | 2 meters | 1 kg | |
| Pendulum C | 1 meter | 2 kg | |
| Pendulum D | 0.5 meters | 1 kg |
Using our knowledge of pendulum physics, we can rank these pendulums according to their maximum speed:
- Pendulum D (highest): The shortest pendulum will have the fastest period and the highest maximum speed. Since it has the shortest length, it will accelerate faster towards the bottom of its arc.
- Pendulum A: This pendulum has a length of 1 meter, making it slower than Pendulum D but faster than Pendulums B and C.
- Pendulum C: Pendulum C has the same length as Pendulum A but is twice as massive. However, mass doesn’t affect the speed, so it will have the same maximum speed as Pendulum A.
- Pendulum B (lowest): The longest pendulum will have the slowest period and the lowest maximum speed.
Tips & Expert Advice for Pendulum Enthusiasts
If you’re interested in experimenting with pendulums, here are a few tips to help you understand their behavior:
- Experiment with length: Create a series of pendulums of varying lengths and observe how their swing periods change. You’ll find that the period increases as the length increases.
- Use a stopwatch or timer: Accurately measure the period of each pendulum to see how it correlates with its length.
- Vary the initial displacement: Observe how the amplitude (maximum displacement) affects the pendulum’s maximum speed. A larger amplitude will result in a higher maximum speed.
- Consider air resistance: In real-world scenarios, air resistance will eventually cause the pendulum’s amplitude and speed to decrease over time. For more accurate observations, reduce air resistance by using a heavier bob or experiment in a vacuum environment.
Understanding pendulums isn’t just about memorizing equations; it’s about experimenting and observing the fascinating interplay of forces in the real world. By changing the length of a pendulum and the angle from which it is released, you can directly observe how these factors influence its speed, creating a satisfying link between theory and practice.
Pendulum FAQs
Here are answers to some common questions about pendulums:
- Q: Is a pendulum’s motion truly simple harmonic motion?
- A: Technically, a pendulum’s motion is only *approximately* simple harmonic motion. The equations describing simple harmonic motion assume a small angle of displacement, where the sine of the angle is very close to the angle itself. At larger angles, this approximation becomes less accurate, and the pendulum’s motion deviates slightly from perfect sinusoidal behavior. However, for small angles, the approximation is very good, and we can use the simple harmonic motion equations to accurately describe a pendulum’s motion.
- Q: Can a pendulum swing forever?
- A: No. In the real world, friction (from air resistance and the pivot point) causes the pendulum to lose energy over time, eventually slowing down and coming to rest. A perfect pendulum, in a vacuum with no friction, would continue swinging indefinitely, but this is an idealized scenario.
- Q: Are pendulums used in any real-world applications?
- A: Yes! Pendulums have a variety of applications, including:
- Clocks: Pendulums are the heart of some of the most accurate clocks, providing a consistent timekeeping mechanism.
- Seismic detectors: Sensitive pendulums are used in seismometers to detect and measure the movement of the Earth, indicating earthquakes and other seismic events.
- Scientific experiments: Pendulums are used in various physics experiments, including investigations of gravity, acceleration, and resonance.
- Therapeutic tools: In some alternative medicine practices, pendulums are used for energy work and dowsing.
Rank Each Pendulum On The Basis Of Its Maximum Speed
Conclusion
The world of pendulums, with their graceful swings and predictable motion, offers a captivating glimpse into the fundamentals of physics. By understanding the factors influencing their speed, we gain a deeper appreciation for the interplay of forces and how they shape the movement of objects around us. As you observe a pendulum swinging, remember that each swing is a fascinating story of energy, force, and the undeniable power of gravity.
Are you interested in learning more about pendulums and their applications? Let us know in the comments below! We’d love to hear your thoughts and questions.






