Remember those geometry classes where you were tasked with calculating the area of shapes? While it may seem like a distant memory, the ability to determine the area of triangles and quadrilaterals is a fundamental skill in many fields, from architecture and engineering to design and even everyday life. But don’t worry, you’re not alone in facing challenges with these calculations. The key to understanding these concepts lies in grasping the formulas and applying them systematically.
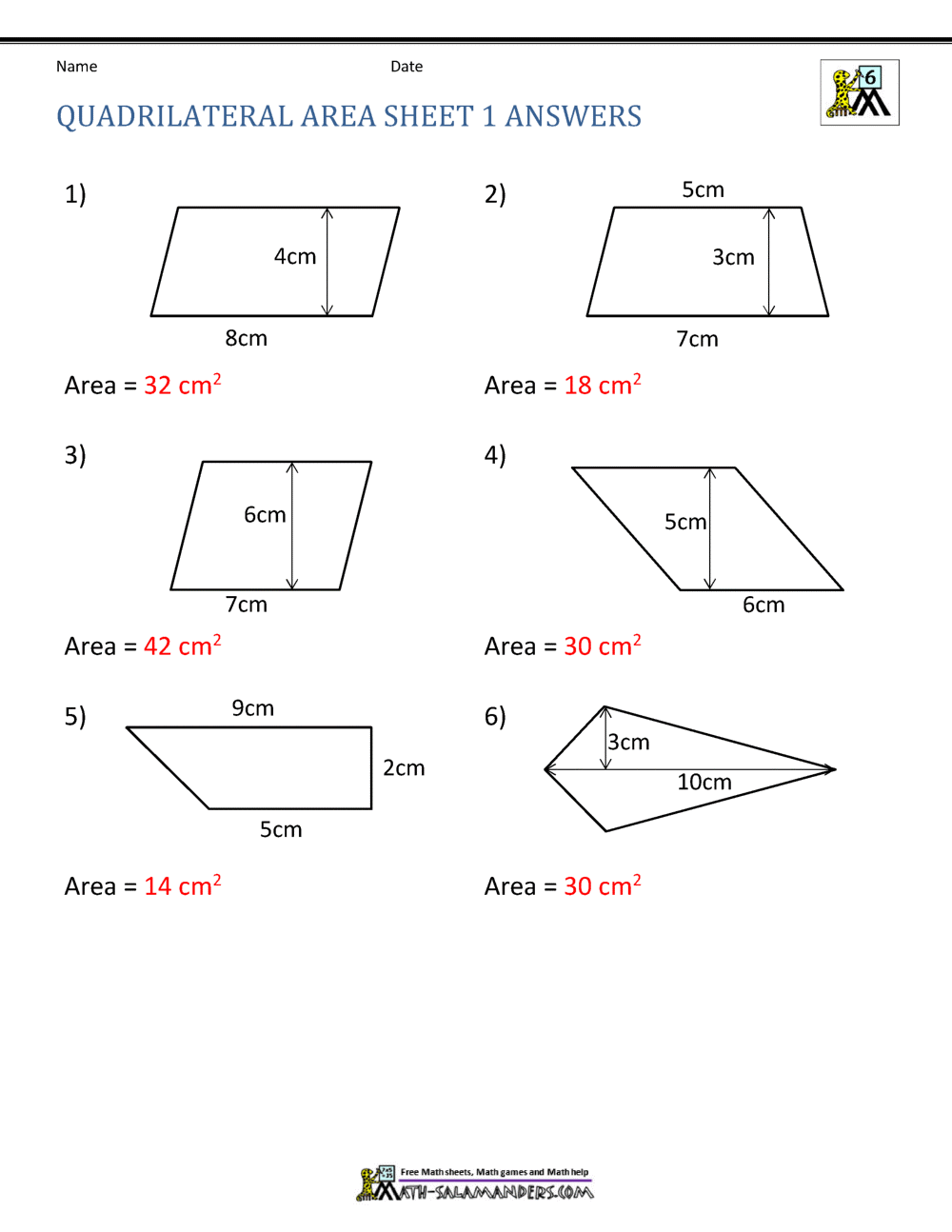
Image: studylistlangdon.z21.web.core.windows.net
This comprehensive guide will provide you with a clear understanding of how to determine the area of triangles and quadrilaterals, providing the much-needed “answer key” to your geometric inquiries. We’ll explore the fundamentals of each shape, discuss the essential formulas, and walk you through step-by-step examples to make these concepts crystal clear.
Unlocking the World of Triangles and Quadrilaterals
The world of geometry is filled with numerous shapes, but triangles and quadrilaterals take center stage for their versatility and practical applications. Triangles, with their three sides and three angles, are the simplest polygons, found in everything from pyramids to bridges. Quadrilaterals, on the other hand, boast four sides and four angles, making them the building blocks of squares, rectangles, and parallelograms, commonly found in architecture and furniture design.
Understanding the area of these shapes is crucial for various tasks. When designing a house, an architect needs to calculate the area of the roof (a triangle) and the floor space (a rectangle) to determine the necessary materials. Similarly, a carpenter needs to calculate the area of a triangular piece of wood to be cut for a specific project.
Triangle Area: Finding the Heart of a Shape
The Formula for Success
The area of a triangle is half the product of its base and height. This can be expressed mathematically as:
Area of Triangle = 1/2 * base * height
Here, the base is the length of any side of the triangle, and the height is the perpendicular distance from the opposite vertex to that side (forming a right angle).

Image: www.traingleworksheets.com
Understanding the Roles of Base and Height
The choice of base and height can vary depending on the triangle’s orientation. You can choose any side as the base, but you must then draw the perpendicular height from the opposite vertex to that side. The height is not always a side of the triangle itself; it can fall inside or outside the triangle depending on its shape.
Examples to Illuminate the Formula
Let’s consider a triangle with a base of 6 cm and a height of 4 cm. Using the formula, we get:
Area of Triangle = 1/2 * 6 cm * 4 cm = 12 cm²
Now, imagine another triangle with a base of 8 cm and a height of 5 cm. We can calculate its area as follows:
Area of Triangle = 1/2 * 8 cm * 5 cm = 20 cm²
These examples help visualize the application of the formula and demonstrate how the area varies with changes in the base and height.
Quadrilateral Area: Demystifying the Four-Sided Shapes
A World of Formulas
Unlike triangles, quadrilaterals have a wider variety of shapes, each with its specific area formula. Here’s a breakdown:
1. Square:
All sides of a square are equal. The area is calculated as follows:
Area of Square = side * side = side²
2. Rectangle:
A rectangle has two pairs of equal sides. Its area is determined by:
Area of Rectangle = length * width
3. Parallelogram:
A parallelogram has two pairs of parallel sides. To find its area, we use:
Area of Parallelogram = base * height
Here, the base is any side of the parallelogram, and the height is the perpendicular distance between that side and the opposite side.
4. Rhombus:
A rhombus has all sides equal and opposite angles equal. Its area can be calculated in two ways:
Area of Rhombus = 1/2 * diagonal 1 * diagonal 2
Or:
Area of Rhombus = base * height
Note that the diagonals bisect each other at right angles, creating four right-angled triangles.
5. Trapezoid:
A trapezoid has one pair of parallel sides. Its area is calculated as follows:
Area of Trapezoid = 1/2 * (base 1 + base 2) * height
Here, base 1 and base 2 are the lengths of the parallel sides, and the height is the perpendicular distance between them.
Applying the Formulas to Real-World Problems
Let’s imagine you’re constructing a rectangular garden bed with a length of 10 meters and a width of 5 meters. Using the formula, the area of the garden bed is:
Area of Rectangle = 10 meters * 5 meters = 50 square meters
Now, suppose you have a rhombus-shaped window with diagonals measuring 6 cm and 8 cm. Using the formula, its area is:
Area of Rhombus = 1/2 * 6 cm * 8 cm = 24 cm²
These examples illustrate how applying the appropriate area formulas can solve real-world problems involving quadrilaterals.
Expert Tips for Mastering Area Calculations
Here are some tips to help you excel at calculating the area of triangles and quadrilaterals:
- Visualize the Shape: Before applying any formula, take a moment to visualize the shape and its properties. Identify the base, height, diagonals, or other relevant parameters.
- Understand the Formula: Make sure you memorize the correct formula for the specific shape you’re dealing with. Be careful not to mix up the formulas for different quadrilaterals.
- Units of Measurement: Always pay attention to the units of measurement used for the side lengths, heights, and diagonals. Ensure they are consistent throughout your calculations.
- Practice Regularly: Like any skill, proficiency in area calculations comes with consistent practice. Work through various problems involving triangles and quadrilaterals of different sizes and orientations.
- Seek Help When Needed: Don’t hesitate to seek assistance if you encounter difficulty. Consult your teacher, tutor, or online resources to clarify concepts and formulas.
By following these tips, you can build a strong foundation in area calculations and confidently tackle any geometric problem involving triangles and quadrilaterals.
FAQ: Common Queries about Area Calculations
1. What is the difference between area and perimeter?
Area refers to the space enclosed within a two-dimensional shape, measured in square units. Perimeter is the total length of all the sides of a shape, measured in linear units.
2. How do I calculate the area of a triangle if I only know the lengths of the sides?
In this case, you can use Heron’s formula, which calculates the area of a triangle based on its side lengths. However, you’ll need to first calculate the semi-perimeter of the triangle (half the sum of its side lengths) before using the formula.
3. Can I calculate the area of a triangle if I don’t know its height?
Yes, if you know two sides and the included angle, you can use the formula: Area = 1/2 * side 1 * side 2 * sin(included angle). Alternatively, you can use Heron’s formula if you know all three side lengths.
4. How do I calculate the area of a quadrilateral if it’s irregular?
For irregular quadrilaterals, you need to divide them into simpler shapes like triangles or rectangles whose areas you can calculate individually. The sum of these areas will give you the area of the irregular quadrilateral.
5. What is the importance of understanding area calculations in real life?
Area calculations are essential for various real-world applications, such as determining the amount of carpet needed for a room, estimating the amount of paint required for a wall, calculating the volume of a container, and designing structures and buildings.
Area Of Triangles And Quadrilaterals Answer Key
https://youtube.com/watch?v=TbKmbke3nv0
Conclusion
Calculating the area of triangles and quadrilaterals is a fundamental skill in geometry and has numerous applications in everyday life. By mastering the formulas, understanding the relationships between base, height, and diagonals, and practicing regularly, you can confidently navigate the world of area calculations. Remember to visualize the shapes, double-check the units of measurement, and seek help when needed. So, are you ready to explore further and dive deeper into the intriguing world of geometric shapes and their areas?






