Have you ever wondered how much space a rectangular box or a can of soup takes up? That’s where the concept of volume comes into play. Understanding volume is not just about filling boxes; it’s a fundamental concept in geometry with applications in everything from architecture to engineering to everyday life.
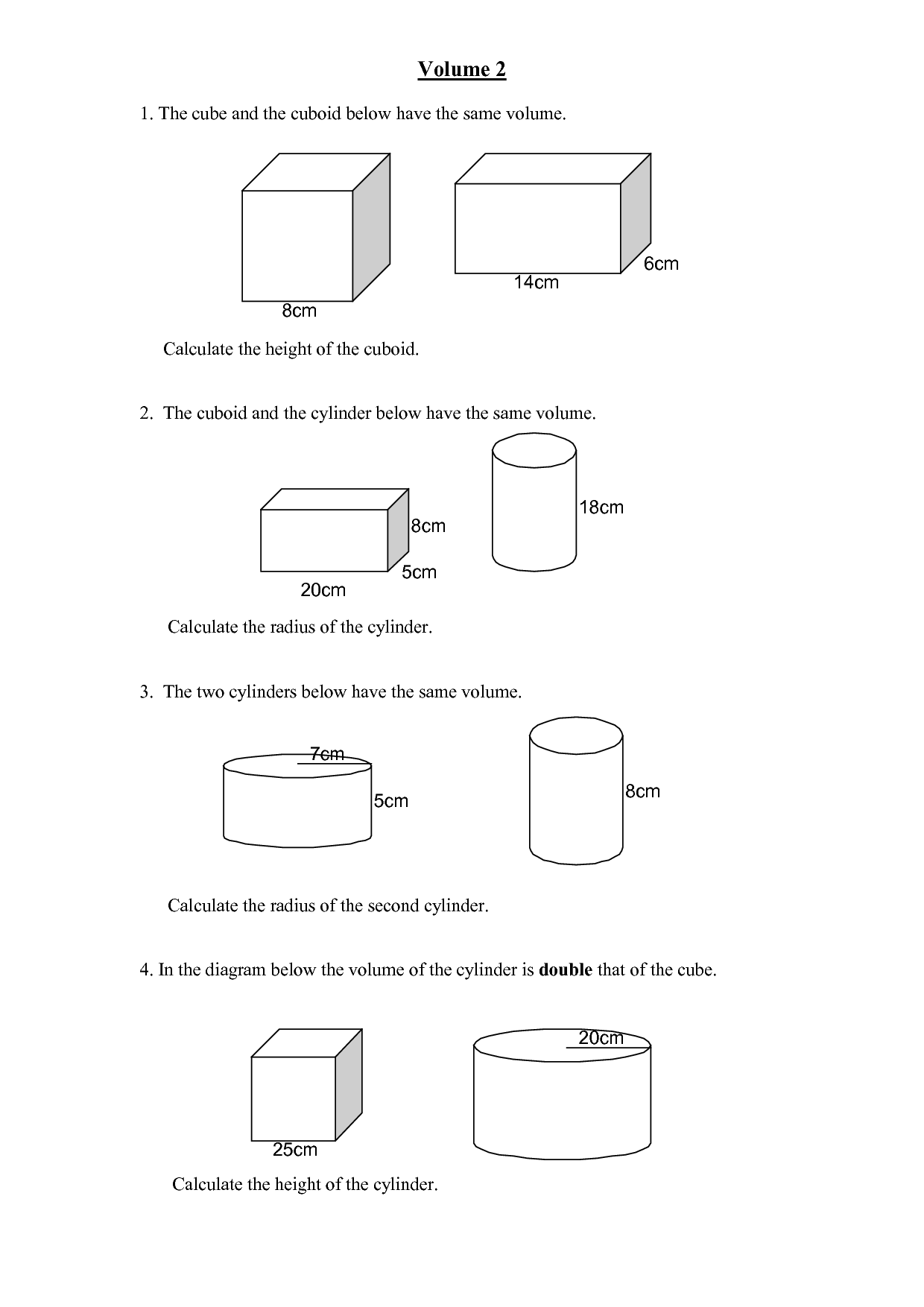
Image: www.worksheeto.com
This guide will delve into the fascinating world of volume, specifically focusing on prisms and cylinders. We’ll unravel the mysteries behind their formulas, explore real-world examples, and help you confidently navigate those challenging volume worksheets. Get ready for an enlightening journey into the realm of three-dimensional geometry!
The Basics of Volume
Volume is the amount of three-dimensional space that a solid object occupies. Imagine filling a container with water; the amount of water that fits inside represents the container’s volume. To measure volume, we use cubic units, such as cubic centimeters (cm³) or cubic meters (m³).
Understanding Prisms
Prisms are three-dimensional shapes with two identical parallel bases and rectangular faces connecting them. The bases can be any shape, like triangles, squares, or even pentagons! Common examples of prisms include:
- Rectangular Prism: A box or a brick
- Triangular Prism: A slice of cake or a tent
- Pentagonal Prism: A prism with a pentagon as its base
Calculating the Volume of Prisms
To find the volume of a prism, we simply multiply the area of its base by its height. Here’s the formula:
Volume of Prism = Base Area × Height
For example, let’s consider a rectangular prism with a length of 5 cm, a width of 3 cm, and a height of 4 cm.
- Base Area: Length × Width = 5 cm × 3 cm = 15 cm²
- Volume: Base Area × Height = 15 cm² × 4 cm = 60 cm³

Image: myans.bhantedhammika.net
Unveiling the Cylinder
A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface. Think of a can of soda or a tube of toothpaste – those are classic examples of cylinders!
Calculating the Volume of a Cylinder
The volume of a cylinder can be calculated using the following formula:
Volume of Cylinder = π × r² × h
Where:
- π (pi): A mathematical constant approximately equal to 3.14159
- r: Radius of the circular base
- h: Height of the cylinder
Let’s say you have a cylinder with a radius of 2 cm and a height of 6 cm.
- Volume: π × 2² × 6 = 3.14159 × 4 × 6 ≈ 75.398 cm³
Tackling Volume Worksheets with Confidence
Now that we’ve covered the fundamentals of volume for prisms and cylinders, let’s equip you with the skills to conquer those daunting worksheets. Here’s a step-by-step guide to make the process smoother:
1. Identify the Shape
The first step is to carefully identify the shape you’re dealing with. Is it a prism or a cylinder? If it’s a prism, what shape is its base?
2. Gather the Necessary Information
You’ll need to determine the dimensions of the shape, which include things like the length, width, height, radius, or the area of the base. These measurements are usually provided in the worksheet.
3. Apply the Correct Formula
Once you’ve identified the shape and collected the required dimensions, select the appropriate volume formula for either a prism or a cylinder.
4. Substitute and Calculate
Plug the dimensions into the formula and perform the necessary calculations. Remember to use the correct units (usually cubic units).
5. Double-Check Your Work
Before moving on, take a moment to review your calculations and ensure the final answer makes sense. Are the units correct? Does the answer seem reasonable in relation to the dimensions?
Real-World Applications of Volume
Volume isn’t just a mathematical concept confined to textbooks. It has numerous practical applications in real life.
- Architecture: Architects use volume calculations to determine the amount of space needed for buildings and rooms, as well as the volume of materials required for construction.
- Engineering: Engineers use volume calculations to design bridges, dams, and other structures, ensuring they can withstand weight and pressure.
- Medicine: Doctors and pharmacists use volume to measure dosages of medications and calculate the volume of fluids administered to patients.
- Cooking: Chefs and home cooks rely on volume measurements for ingredients, ensuring recipes are accurately prepared.
- Everyday Life: We use volume every day when we fill containers with liquids, calculate the amount of fuel in a car, or estimate the space needed to store items.
Additional Tips for Success
Here are some extra tips to make your volume calculations even smoother:
- Use a Calculator: For more complex calculations, a calculator can be your best friend.
- Draw Diagrams: Visualizing the shapes can help you understand the relationships between their dimensions.
- Practice: The more you practice, the more comfortable you’ll become with calculating volumes.
- Seek Help When Needed: Don’t be afraid to ask for clarification from your teacher or a tutor if you’re struggling with a particular concept.
Volume Prisms And Cylinders Worksheet Answer Key
Conclusion
Mastering the concepts of volume for prisms and cylinders will not only help you excel in geometry but will also provide you with valuable skills applicable to various fields and everyday life. Remember, the key to success is understanding the formulas, practicing with worksheets, and applying your knowledge to real-world scenarios. So, delve into the fascinating world of volume, conquer those worksheets, and unlock the secrets of this essential geometrical concept!






