Have you ever looked up at a firework display and wondered about the beautiful, symmetrical arcs the rockets trace across the night sky? Or perhaps you’ve been captivated by the graceful curve of a suspension bridge, a shape that seems to defy gravity itself. These are just a few examples of parabolas in action, a fundamental shape in mathematics with surprising applications in both the natural and man-made worlds.
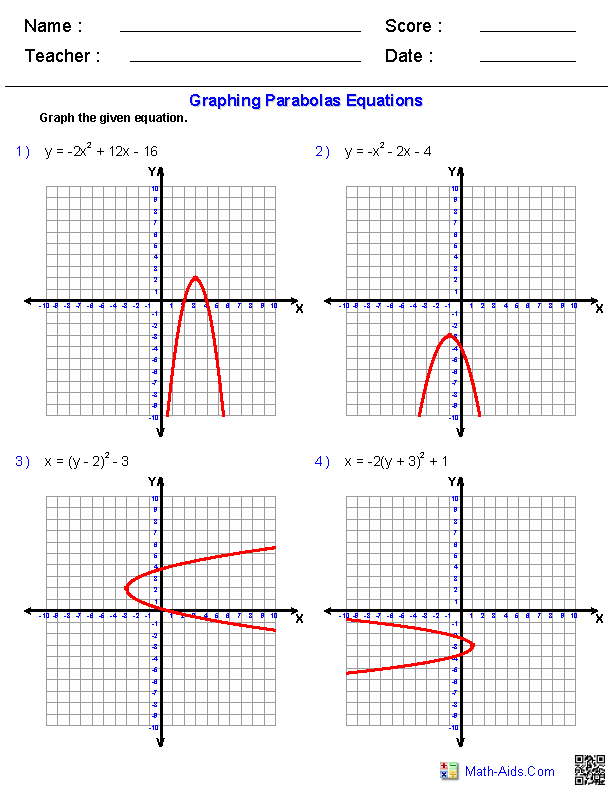
Image: www.math-aids.com
Understanding parabolas is not just about solving equations or memorizing formulas. It’s about delving into a fascinating realm of geometry and its connection to the physical world. It can unlock the secrets of projectile motion, help us design better antennas, and even explain the orbits of celestial bodies. This guide will provide you with a comprehensive understanding of parabolas, from their basic definition and properties to real-world applications and valuable exercises for practice.
What is a Parabola?
In its purest form, a parabola is a symmetrical, open curve defined by a specific mathematical equation. Imagine a point (called the focus) and a line (called the directrix) that are a certain distance apart. A parabola is the set of all points that are equidistant to both the focus and the directrix. This unique relationship creates the characteristic “U” shape that we associate with parabolas.
Key Properties of Parabolas
Focus and Directrix
The focus is a fixed point that lies inside the parabola’s curve. A crucial property of a parabola is that all points on the curve are equidistant from the focus and the directrix, a line that lies outside the curve. This relationship defines the parabola’s shape.
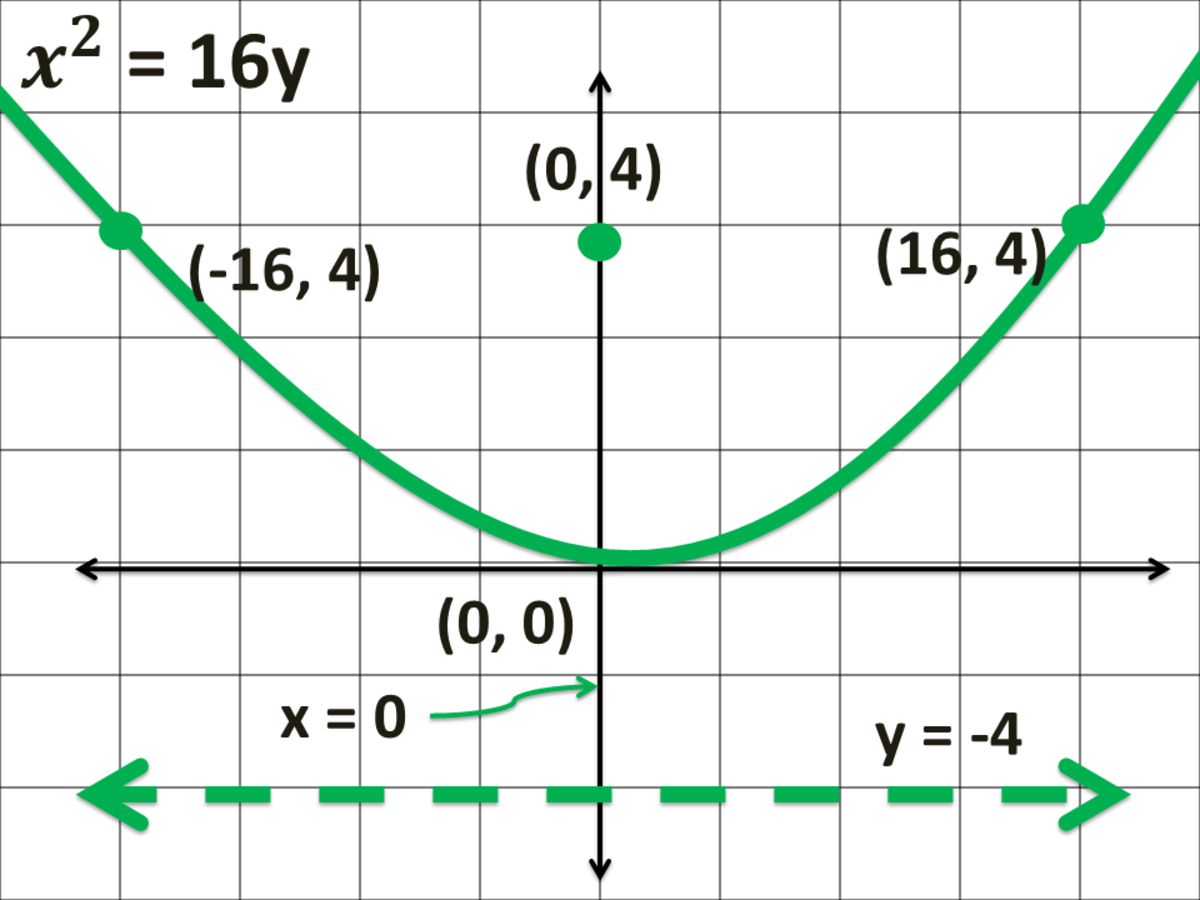
Image: owlcation.com
Vertex
The vertex is the point on the parabola where it intersects its axis of symmetry. It’s the lowest point (or highest point, depending on the orientation) of the parabola. The vertex is also the midpoint between the focus and the directrix.
Axis of Symmetry
The axis of symmetry is a line that divides the parabola into two symmetrical halves. It passes through the vertex and the focus.
Standard Equation
The equation of a parabola is determined by its orientation and the location of its vertex and focus. The standard form of a parabola opening to the right is:
(y – k)² = 4p(x – h)
Where:
- (h, k) are the coordinates of the vertex
- p is the distance between the vertex and the focus
Similarly, a parabola opening to the left, upwards, or downwards can be represented by different standard forms.
Parabolas in Action: Real-World Applications
1. Reflecting Telescopes
The parabolic shape of a reflecting telescope’s primary mirror plays a crucial role in collecting and focusing light from distant celestial objects. This shape ensures that all parallel rays of light entering the telescope converge at a single point, the focus, creating a clear and magnified image.
2. Satellite Dishes
Satellite dishes are another excellent example of parabolic principles. The dish’s curved shape reflects incoming radio waves from a satellite, focusing them onto a receiver at the focal point. This allows for efficient reception of weak signals from far-off satellites.
3. Projectile Motion
Understanding parabolic motion is essential in fields like physics and engineering. When an object is launched into the air, its trajectory, neglecting air resistance, forms a parabolic path. This knowledge is vital for calculating the range and height of projectiles, from rockets to baseballs.
Parabola Questions and Answers PDF Download: Your Resource for Mastery
Now that you have a basic understanding of parabolas, you’re probably ready to dive into exercises and practice questions. A valuable resource for this is a “Parabola Questions and Answers PDF Download,” which provides a comprehensive collection of problems and their solutions. These pdfs can be a tremendous tool for:
- Reinforcing your understanding of key concepts: Working through practice problems can solidify your understanding of basic definitions, equations, and properties of parabolas.
- Building problem-solving skills: The pdfs offer a wide range of problems, ranging from simple applications to more complex scenarios, allowing you to develop your problem-solving strategies.
- Preparing for exams and assessments: Practice questions help you familiarize yourself with the types of problems you might encounter on tests and improve your confidence in tackling them.
Where to Find Parabola Questions and Answers PDF Download
Here are some common places you can find “Parabola Questions and Answers PDF Download” resources:
- Online Textbook Resources: Many online textbook platforms offer free or paid access to practice problems and solutions, including those related to parabolas.
- Educational Websites: Several websites dedicated to math education provide free downloadable resources, such as pdfs containing practice questions.
- Academic Search Engines: Search engines like Google Scholar can help you find academic articles and research papers that often include supplemental material, including practice problems, in downloadable formats.
- Textbook Companion Websites: Your textbook might have a companion website that offers additional resources, including practice problems and answer keys in downloadable formats.
Parabola Questions And Answers Pdf Download
Conclusion
Parabolas are a fascinating and fundamental concept in mathematics with a wide range of real-world applications. Understanding their properties and equations can unlock a deeper appreciation for their role in shaping our world. By dedicating time to exploring practice problems and seeking out resources like “Parabola Questions and Answers PDF Download,” you can build a solid foundation of knowledge and excel in your understanding of this crucial mathematical element. So take the leap, delve into the world of parabolas, and discover the secrets they hold.






